Wirbelstromverluste (WSV)
Mathematische Beschreibung der Wirbelstromverluste und die Simulation über der Drehzahl.
Die Messungen an Servomotoren deuten darauf hin, dass sich die Wirbelstromverluste (in Abhängigkeit der Drehzahl) NICHT durch ein Polynom abbilden lassen. In deren Auswertung lässt sich der Verlauf der Ableitungen bei kleinen Drehzahlen (insbesondere bei kalten Motoren) nicht erklären. Die Näherung über das Polynom lässt sich lediglich für die Darstellung der drehzahlabhängigen Verluste in [W] nutzen.
Es wurde deshalb nach einer Methode gesucht, die das Verhalten der ersten Ableitung = Drehmoment in [Nm] und der zweiten Ableitung = VISCOUS DAMPING in [Nm/RPM] besser beschreibt.
A) Abhängigkeit von der Temperatur
Die Auswertungen aus dem Austrudelversuch zeigen eine deutliche Abhängigkeit von der Blech-Temperatur. Deshalb wurde im Ansatz 1 versucht, diesen Einfluß deutlich zu machen:
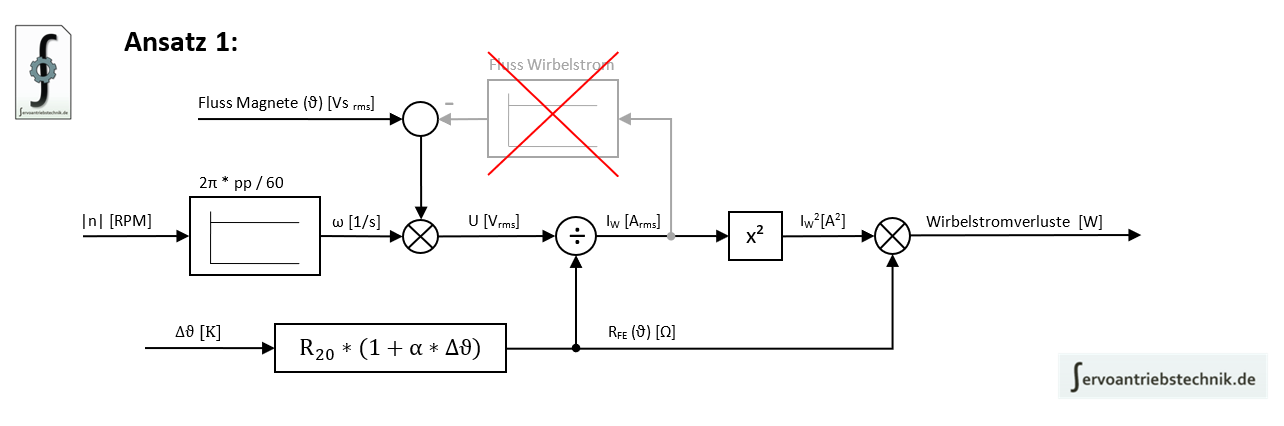
Für Drehmomente kleiner Mo und Leerlauf ist die Amplitude des Gesamtflusses dominiert vom Fluss der Magnete. Rotieren die Magnete mit der Drehzahl n, wird in jedem Blech eine treibende Spannung induziert, die einen Wirbelstrom hervorruft. Die Summe aller Wirbelströme ist Abhängig von der Eisentemperatur. Multipliziert mit dem ohmschen Widerstand des Eisens ergibt das Quadrat der Wirbelströme die Wirbelstromverluste in [W].
Kennt man die Wirbelstromverluste [W] bei einer bestimmten Drehzahl, kann der Regelkreis leicht normiert werden.
Liegen Messungen bei verschiedenen Blech-Temperaturen vor, kann die gemessene Abhängigkeit hier bestätigt werden. (Achtung, Magnete selbst sind ebenfalls temperaturabhängig (NdFeB: -8% bis -15% pro +100 Kelvin). Nur Datenblattangaben verwenden. Keine Ergebnisse verwenden, die durch Messungen bei hohen Drehzahlen ermittelt wurden. Diese Ergebnisse können gerade durch den Einfluss der Wirbelströme verfälscht sein).
Temperaturkoeffizient Wirbelstrom-Verluste WSV :
Die Wirbelstromverluste sind bei ca. 30°C um Faktor 1,6 höher als bei 130°C. Die Abnahme der Wirbelstromverluste von ca. 30°C -> 130°C ergibt damit den Faktor 1/1,6 = 0,625.
Der Temperaturkoeffizient von Eisen beträgt 0,005 - 0,0065 / Kelvin. Setzt man den Temperaturkoeffizient in die oben dargestellte Regelstruktur ein, erhält man bei 100 K Übertemperatur (1/1,6)² x 1,6 = 1/1,6 = 0,625.
Für die Wirbelstromverluste in [W] beträgt der Temperaturkoeffizient ca. -0,006 / Kelvin => -6% pro +10 Kelvin
![Wirbelstromverluste [%] vs. Temperatur [°C]](../../../attachments/Image/Wirbelstromverluste-vs.-Temperatur-degC.PNG?template=generic)
Rück-Kopplung:
Die Messungen zeigen, dass im unteren Drehzahl-Bereich - insbesondere bei kalten Motoren - die Wirbelstromverluste eher mit dem Exponent n^1,6 ansteigen. => Die Ableitung VISCOUS FRICTION [Nm] wächst dann mit Exponent n^0,6. Im oberen Drehzahl-Bereich scheint es, als würde die Ableitung zunächst in eine lineare Steigung übergehen. Das lässt eine Art Sättigung oder Rückkopplung (Skin-Effekt) vermuten.
Ansatz 1 enthält deshalb eine Rückkopplung, die das Erregerfeld der Wirbelströme schwächt*². Gäbe es diese Schwächung des Feldes, müsste auch die induzierte Spannung der Wicklung mit der Drehzahl deutlich sinken. Die Drehzahl-Konstante KE [V / 1000 RPM] bleibt aber nahezu konstant. Zur Deckung der Verluste steigt lediglich der Strombedarf in Q-Richtung leicht an. PWSV = Iq*UEMK
Die Rückkopplung in Ansatz 1 ist für eine überschlägige Simulation der Wirbelstromverluste im Blech nutzbar, aber NICHT korrekt.
Erkenntnis aus Ansatz1:
- lineare Proportionalität mit dem Temperaturkoeffizient (für kleine n)
- Probe oder Kontrolle der berechneten Verluste ist möglich über PWSV = PΩ = U*I oder I²*R oder U²/R oder I*ψ*2π*n
- Die Simulation verwendet die Eingangsgröße Drehzahl n [RPM] zunächst quadratisch
- Die Simulation verwendet die Eingangsgröße Fluss ψ [Vs] zunächst quadratisch
B) Filterzeitkonstante
Tiefpass-Filter 1.Ordnung mit -20 dB/Dekade:
Im zweiten Ansatz wird die induzierte Spannung im Blech nicht durch den rein ohmschen Widerstand kurzgeschlossen, sondern durch eine Reihenschaltung aus R und L.
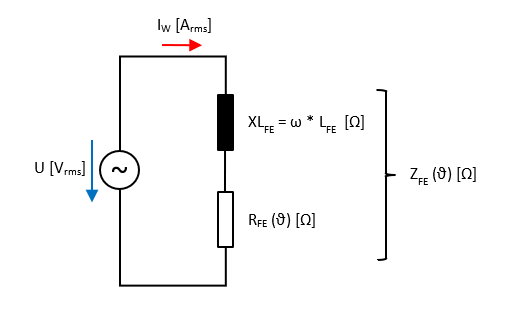
Hinweis 1: siehe auch Kapitel "Kurzschluß-Bremsung" und Widerstands-Bremsung von Servomotoren
Hinweis 2: für Ansatz 2 und folgende, wurde die Motor-Polpaarzahl pp bewußt eliminiert, da die Induktivität und der Widerstand - für dem Wirbelstrom im Blech - reine Rechengrößen darstellen und durch die Messung der Verluste in [W] bestimmt werden.
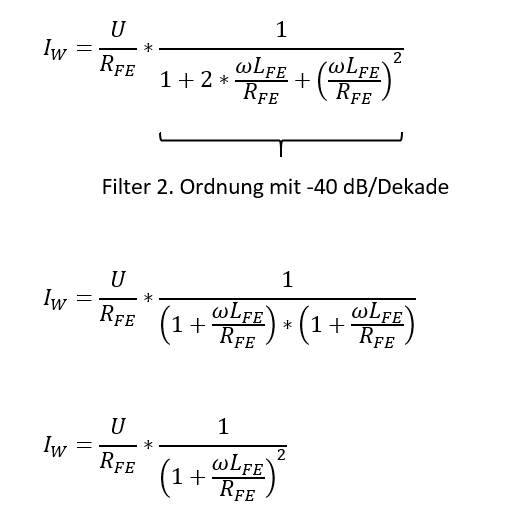
In der Nachrichentechnik wird das Tiefpass-Filter 1.Ordnung üblicherweise dargestellt in der Form:
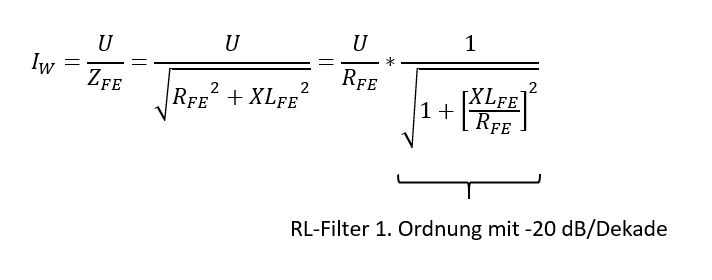
Durch das WARM-KLALT-Verhalten des Widerstandes verändert sich nicht nur die Amplitude, sondern auch die Zeitkonstante.
Mit Verwendung des Filters wird die Simulation modifiziert zu:
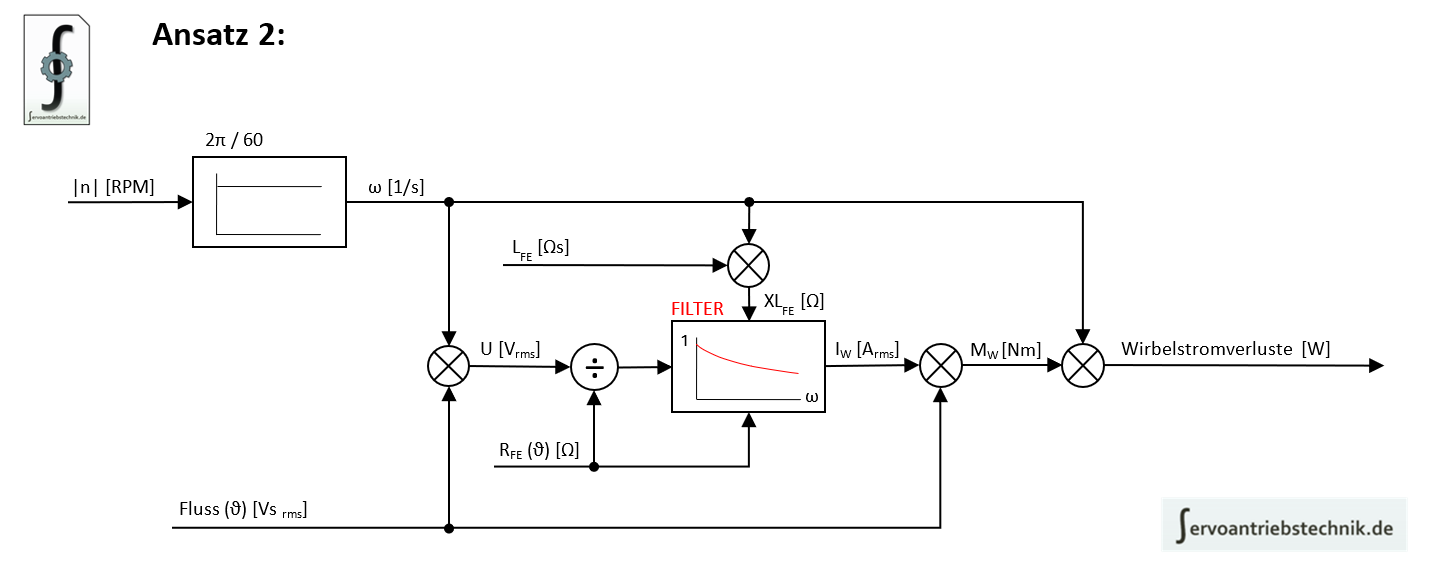
Tiefpass-Filter 2.Ordnung mit -40 dB/Dekade:
Die Ergebnisse der Simulation nach Ansatz 2 sind recht brauchbar. Für kalte Motoren ergibt sich aber im unteren Drehzahlbereich eine Abweichung zu den Messdaten. Diese kann durch die Verwendung eines Filters 2. Ordnung minimiert werden (Ansatz 3).
Ermittlung der verwendeten Größen
Für die Simulation müssen die Startwerte für den Fluss Ψ, den Widerstand R und die Induktivität L gefunden werden. (folgt)
C) Ergebnisse der Simulation:
Die og. Regel-Struktur kann durchaus zur Simulation der Gesamt-Verluste (ausgenommen Kupferverluste) verwendet werden. Die Präzision der Simulation im Vergleich zu den Messdaten ist erstaunlich hoch, wie folgende Auswertung zum Austrudelversuch bei 25-30°C im Vergleich zum Austrudeln bei 125°C-130°C zeigt:
TIP: Messen Sie kurz vor dem Deaktivieren des Servoverstärkers den Leerlauf-Strom I LL [A]. Diese Messpunkte können Sie in die Auswertung aufnehmen.
Ergebnis der Messung & Simulation (hot 125-135°C):
Messung & Simulation der Verluste in [W]:
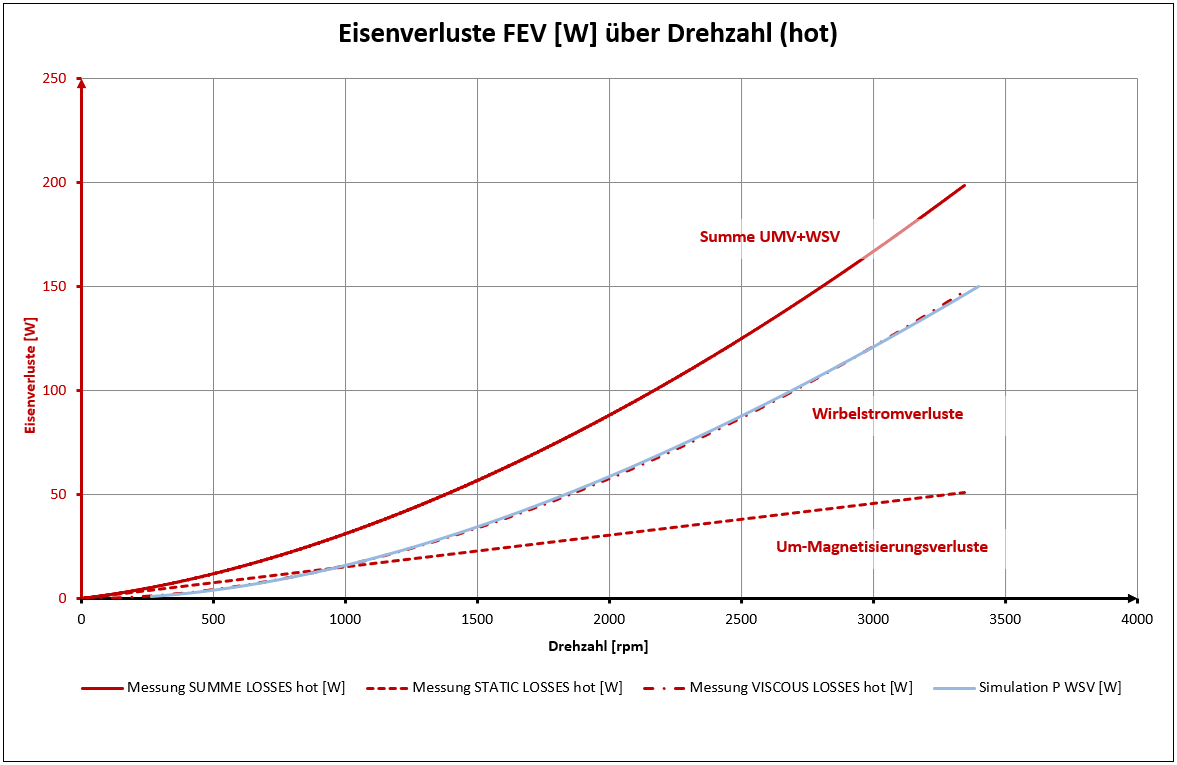
Erstaunlich gute Übereinstimmung der Simulation mit dem Messergebnis auch bei der ersten Ableitung VISCOUS FRICTION [Nm] und der zweiten Ableitung VISCOUS DAMPING [Nm/kRPM]:
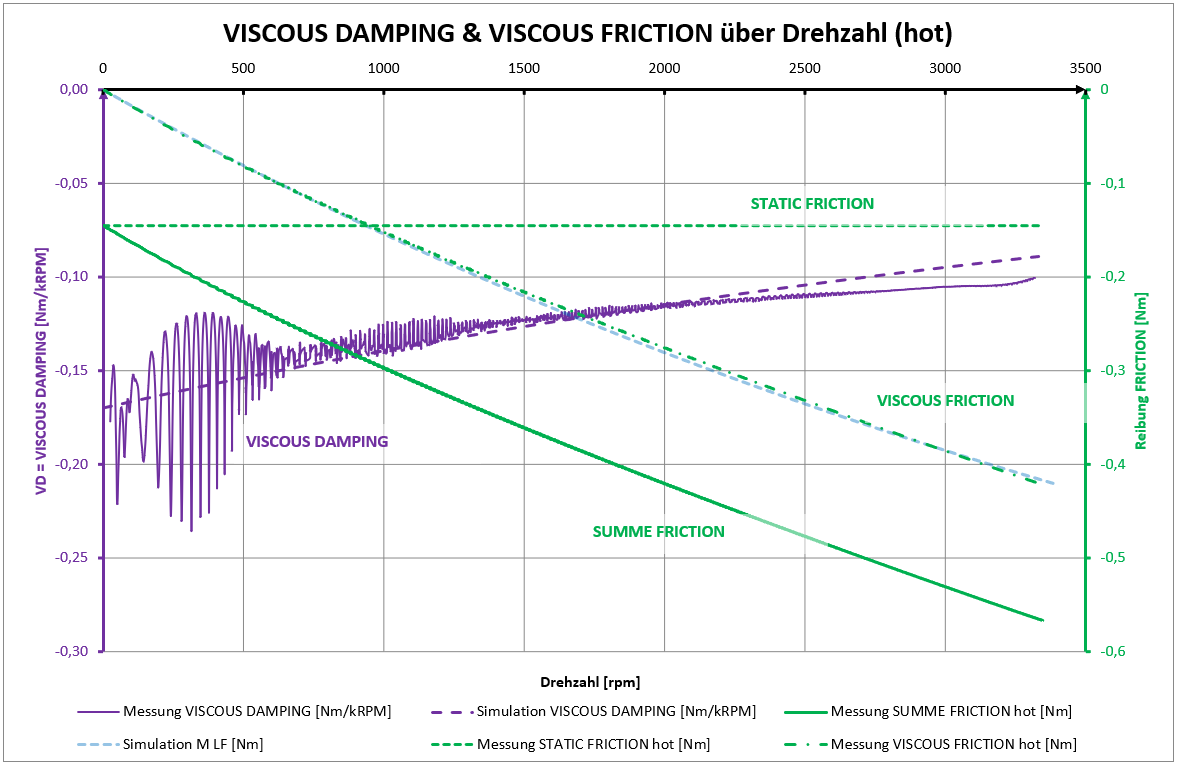
Ergebnis der Messung & Simulation (kalt 25-35°C):
Messung & Simulation der Verluste in [W]:
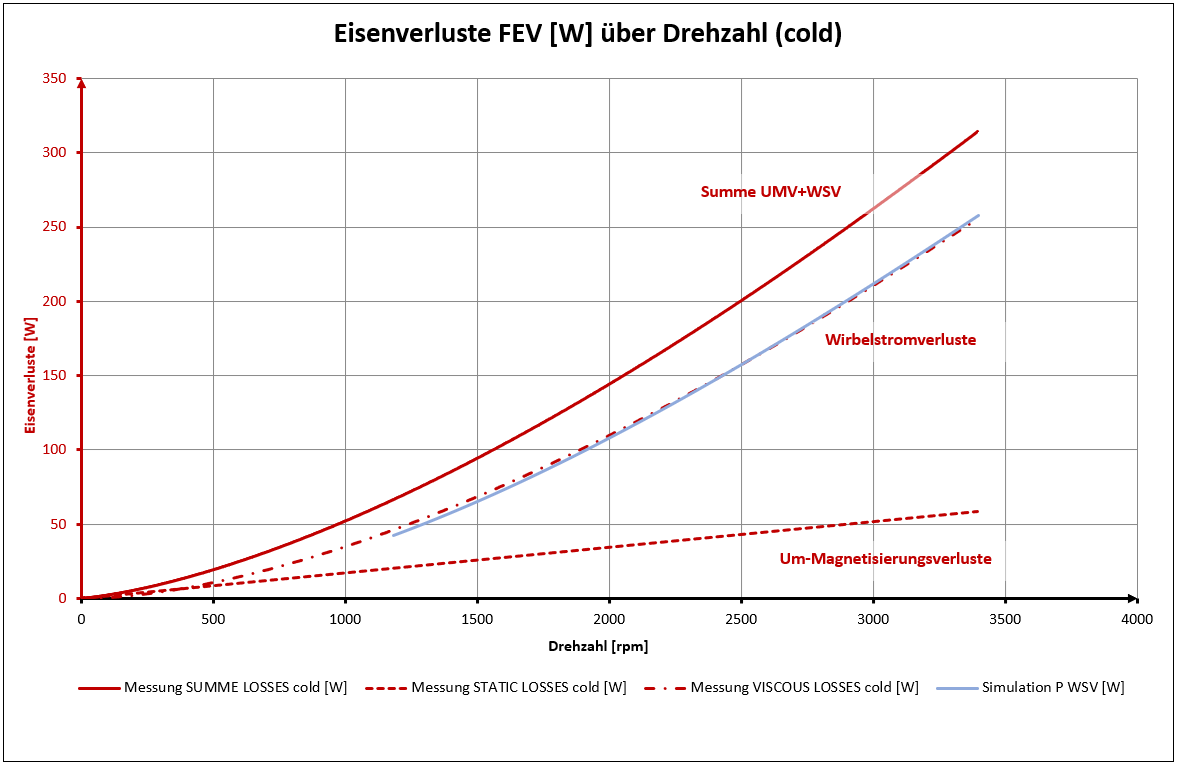
Im kalten Zustand zeigt Simulation bei niedrigen Drehzahlen eine Abweichung zu dem Messergebnis bei den Ableitungen VISCOUS FRICTION [Nm] und VISCOUS DAMPING [Nm/kRPM]:
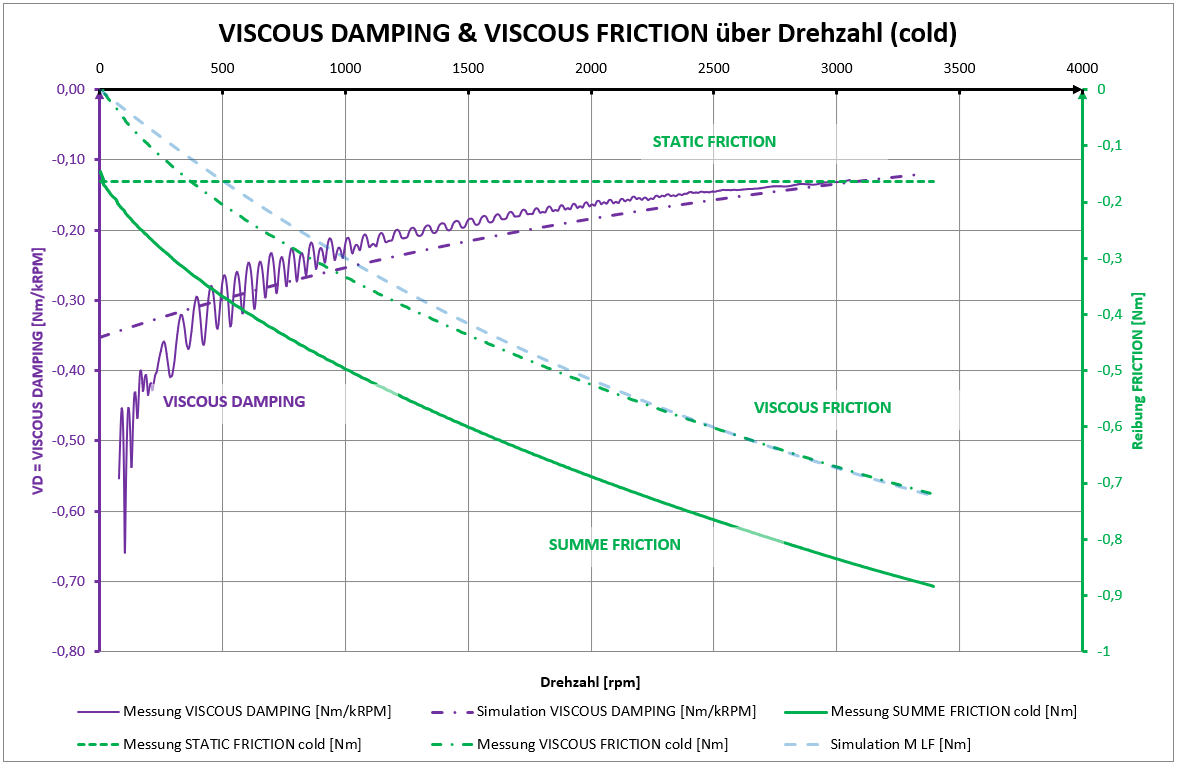
Falls Sie hierzu eigene Untersuchungen anstellen, bitte teilen Sie Ihre Ergebnisse mit mir. Herzlichen Dank.
Anmerkung des Autors:
An dieser Stelle enden zunächst meine Untersuchungen zum Thema "Eisenverluste". Die Ziele waren lediglich:
- Zur Berechnung der S1-100K-Kennlinie des Dauer-Drehmoments von Servomotoren sollte die Abhängigkeit der Eisenverluste (hot) über der Drehzahl möglichst genau bestimmt werden.
- Für die thermische Nachführung der Optimierungs-Vorschrift bei der Wirkungsgrad-Optimierung sollte die Abhängigkeit der Eisenverluste von der Motor-Temperatur bekannt sein.
- In beiden Fällen sind Querströme kleiner Io gegeben, deshalb wurde der Einfuß hoher Querstöme im S3-Aussetzbetrieb auf die Eisenverluste nicht berücksichtigt.
Fußnote *²:
Die maximale Fluss-Änderung ist in Q-Richtung. Die Wirbelströme fliessen nicht im Kupfer, sondern im Eisen in negativer Q-Richtung und erzeugen (in Analogie zu einem negativen Q-Strom im Kupfer) ein Bremsmoment. Das Erregerfeld ψPM und das Gesamtfeld ψµ erfährt durch die Wirbelströme und den Remanenz-Schweif eine zunehmende Verzögerung, was zu einer Verdehung des Feldwinkels gegen die Rotation führt. Das entspricht einer Zunahme des Kommutierungs-Winkels (90° + Δφ). Es muß also zwangsläufig ein positiver Q-Strom im Kupfer (zur Deckung der Wirbelstromverluste) fließen, der den negativen Quer-Strom im Eisen kompensiert.
30.07.2018 Roland Fetzner