Polynom 7. Ordnung
Wer sich mit Bewegungs-Gesetzen befasst, der kennt sicherlich das ruckfreie, symmetrische Polynom 7. Ordnung. Diese Trajektorie wird in der Regel für "Rast in Rast"- Positionierung verwendet.
Wegen des relativ großen Verschliffs, regt es die Schwing-Neigung einer elastischen Mechanik wenig an.
Wer mit Schwingungen während der Zieleinfahrt zu kämpfen hat, sollte sich zusätzlich mit den voreilenden Polynomen 7. Ordnung befassen. Im Folgenden werden einige Varianten des Polynoms 7. Ordnung vorgestellt:
Koeffizienten des Polynoms 7. Ordnung:
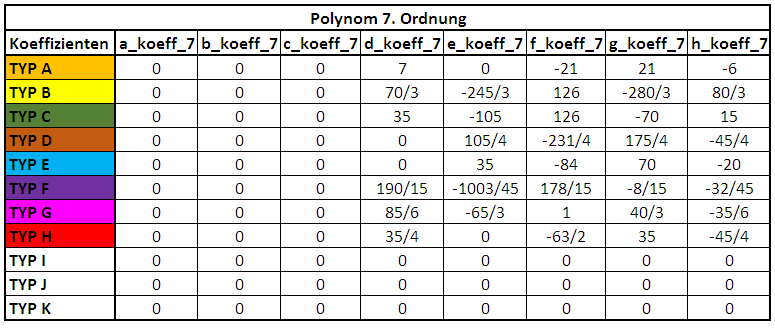
Eigenschaften des Polynoms 7. Ordnung:
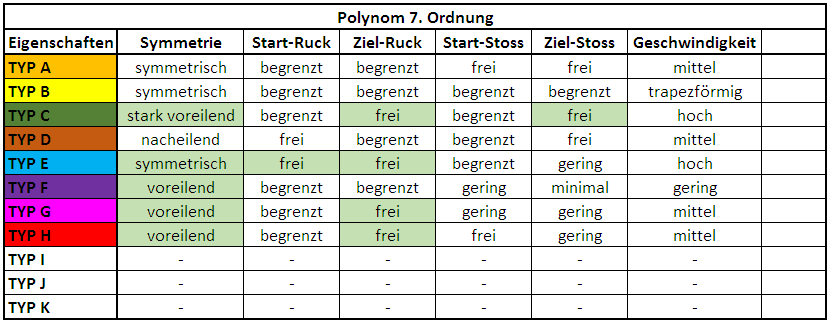
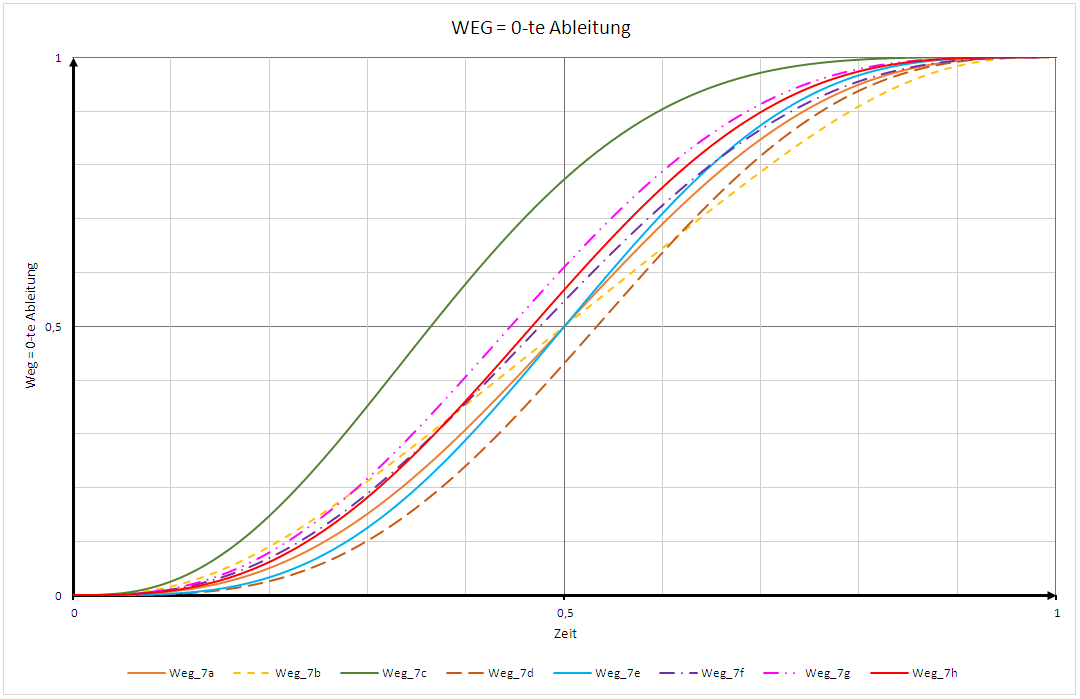
WEG Polynom 7. Ordnung:
s (t) = a_koeff + b_koeff * t + c_koeff * t^2 + d_koeff * t^3 + e_koeff * t^4 + f_koeff * t^5 + g_koeff * t^6 + h_koeff * t^7
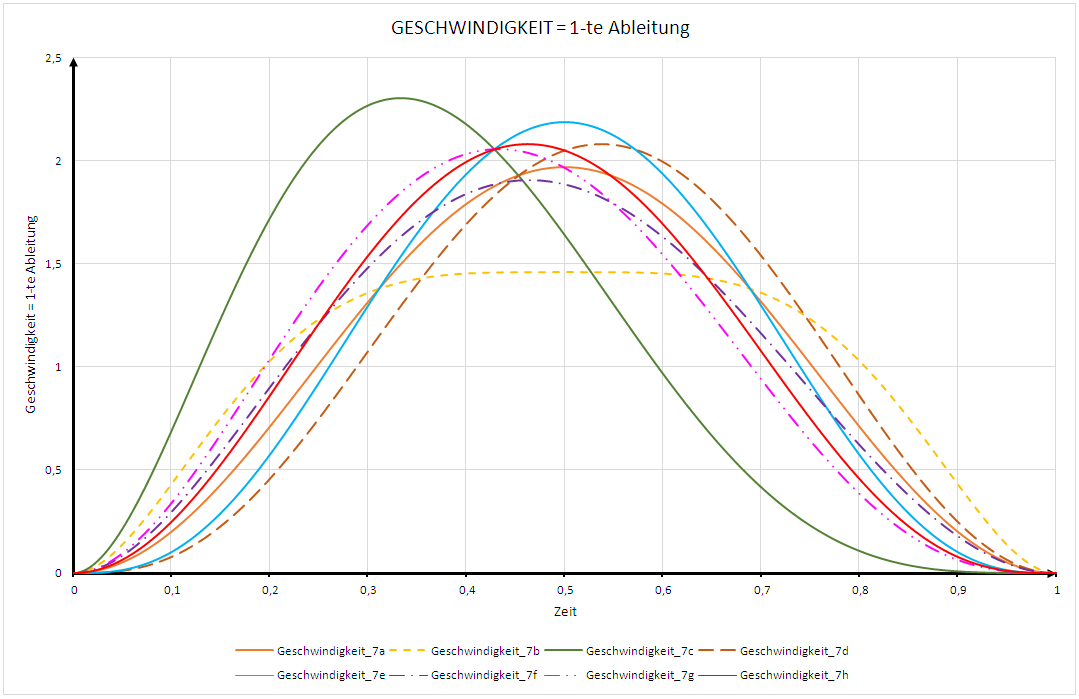
GESCHWINDIGKEIT Polynom 7. Ordnung:
v (t) = b_koeff + 2 * c_koeff * t + 3 * d_koeff * t^2 + 4 * e_koeff * t^3 + 5 * f_koeff * t^4 + 6 * g_koeff * t^5 + 7 * h_koeff *t^6
BESCHLEUNIGUNG Polynom 7. Ordnung:
a (t) = 2 * c_koeff + 6 * d_koeff * t + 12 * e_koeff * t^2 + 20 * f_koeff * t^3 + 30 * g_koeff * t^4 + 42 * h_koeff * t^5
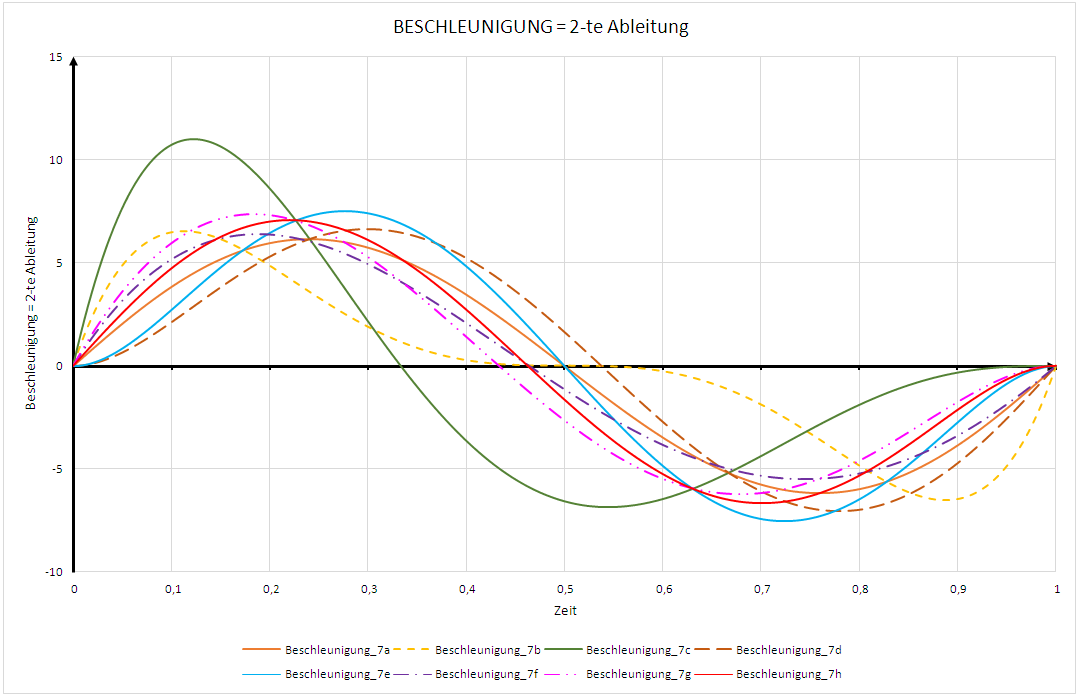
RUCK Polynom 7. Ordnung:
r (t) = 6 * d_koeff + 24 * e_koeff * t + 60 * f_koeff * t^2 + 120 * g_koeff * t^3 + 210 * h_koeff * t^4
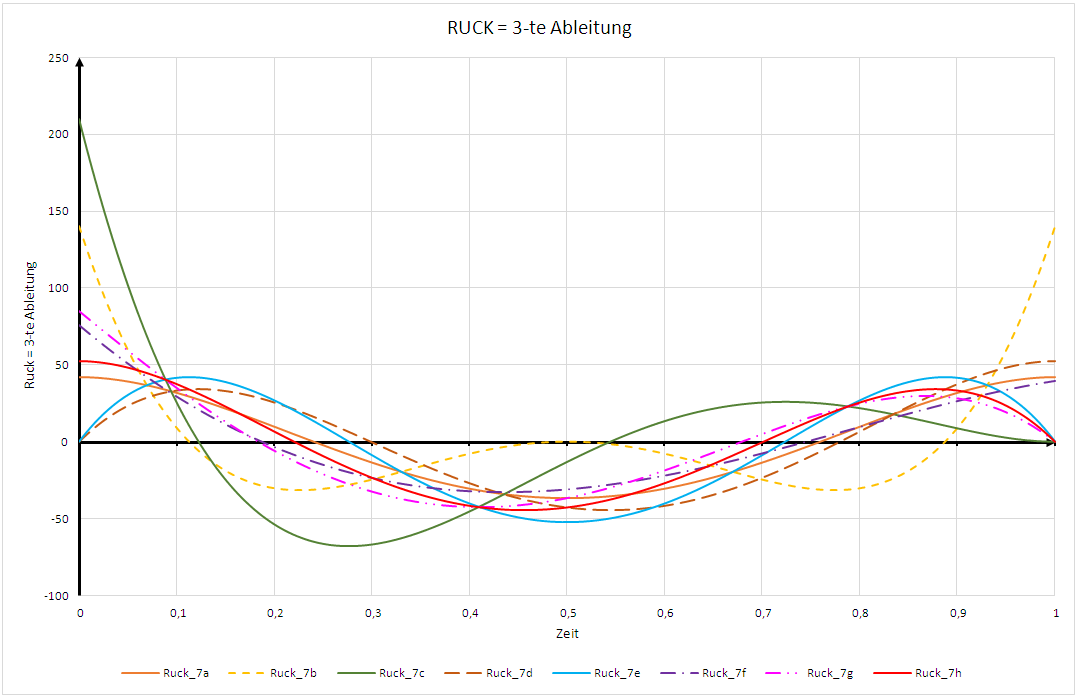
STOSS Polynom 7. Ordnung:
r' (t) = 24 * e_koeff + 120 * f_koeff * t + 360 * g_koeff * t^2 + 840 * h_koeff * t^3
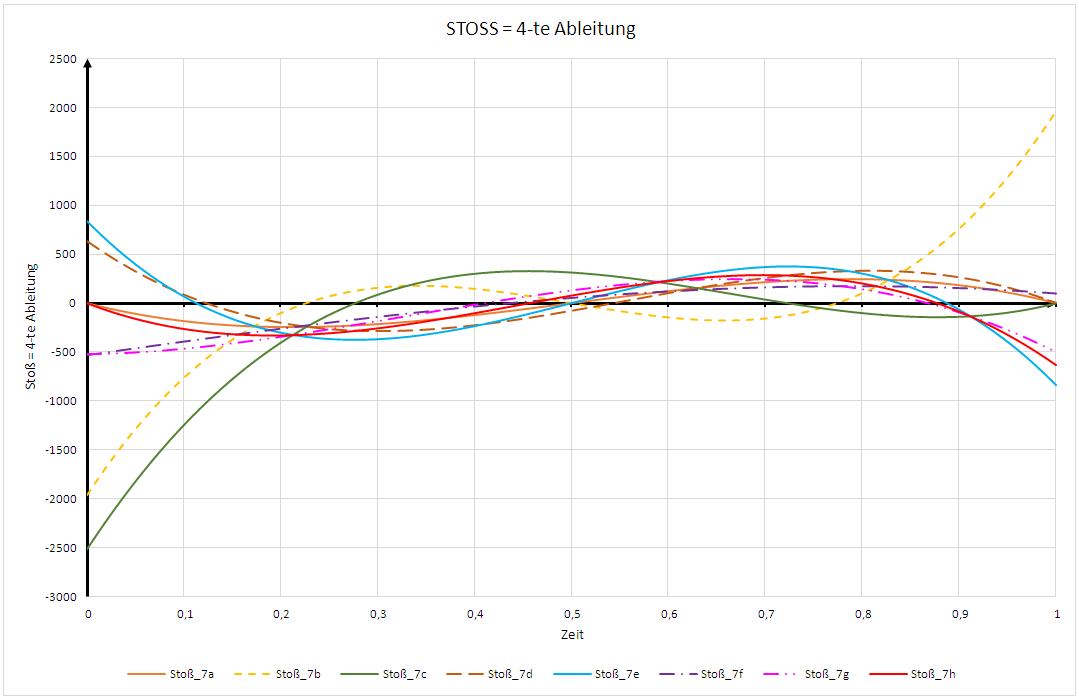
Welche Ergebnise die verschiedenen Typen hinsichtlich der Anregung von Schwingungen liefern, kann im Simulator 1-Massen-System und Simulator 2-Massen-System getestet werden.
Diese EXCEL-Studie zum Polynom 7. Ordnung kann hier geladen werden:
Das EXCEL-Tool zur automatisierten Bestimmung der Koeffizienten von Polynomen bis 9. Ordnung:
Polynom x-ter Ordnung V1.03.xls
23. März 2018
R. Fetzner