Kurzschluß-Bremsung & Widerstands-Bremsung

Die Kurzschluß-Bremsung oder Widerstands-Bremsung kann in Stern-Schaltung oder Dreieck-Schaltung realisiert werden. Die Berechnungen im Tool Drehzahl-Drehmoment-Kennlinie V4.xx.xlsm wurden für Beschaltung im Stern durchgeführt:

Kurzschluß-Bremsung oder Widerstands-Bremsung in Stern-Schaltung

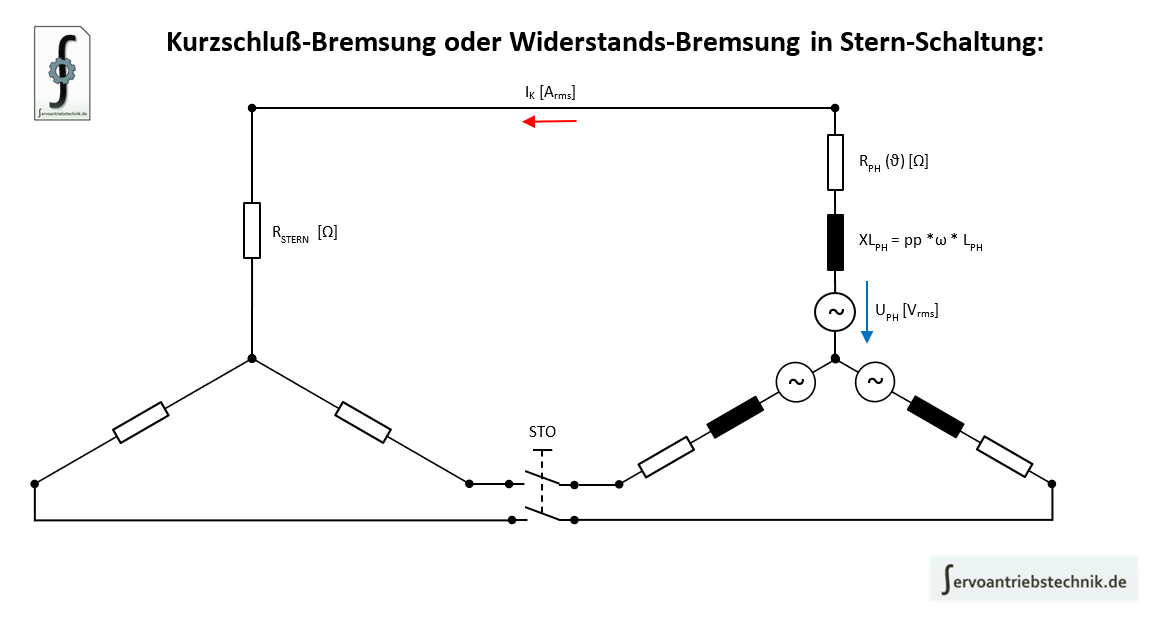
In Abhängigkeit des Brems-Widerstands ändert sich die Zeitkonstante für den Kurzschluß-Strom und damit der Bremsmomentverlauf über der Drehzahl.

Kurzschlußstrom und Bremsmoment

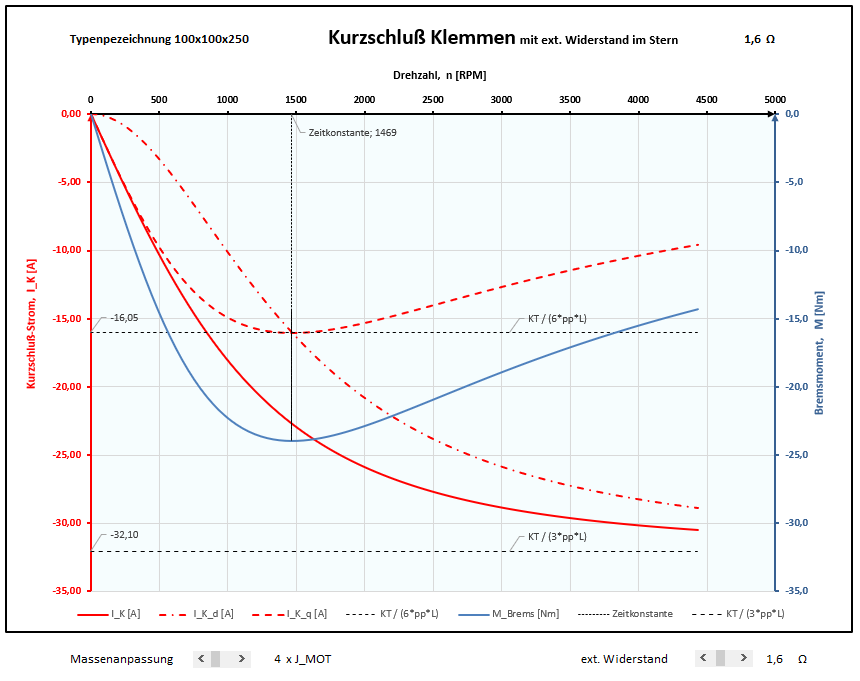
Erkenntnisse aus der Herleitung (Ld ≈ Lq):

• Maximales Bremsmoment liegt vor, wenn der Phasenstrom 45° im 3. Quadranten des dq-Koordinaten-System einnimmt.
• Daraus folgt für die Widerstände (R PH + R EXT) = XL = pp*ω*LPH und für die Ströme -Iq = -Id und IPH = SQRT(2)* Iq
• Die Amplitude des Quer- und Längsstroms -Iq = -Id ist bei 45° NICHT abhängig vom externen Widerstandwert und ist immer KT / (6*pp*LPH) also IPM /2
• Das Bremsmoment lässt sich über die Drehzahl berechnen mit MB (n) = Iq (n) * KT und ist bei 45° maximal -> MB Max = KT² / (6*pp*LPH)
• Damit lässt sich auch das maximale Bremsmoment nicht über die ohmsche Beschaltung einstellen - es sei denn - man wählt den Widerstand so groß, daß die Zeitkonstante höher als die maximale Betriebsdrehzahl ist.
• Der Anhalteweg ist bestimmt durch die Bremsarbeit während der Bremszeit [Ws] = Bremsleistung [W] * Anhaltezeit [s] = Moment [Nm] *ω [1/s] * Anhaltezeit [s] somit der Fläche unter dem Bremsmomentverlauf.
• Die Bremsleistung (n) lässt sich berechnen mit PB (n) = 3 * IPH² (n) * (R PH + R EXT) oder über PB (n) = Iq (n) * KT * ω
• Kürzeste Anhaltezeit ist gegeben, wenn der Wendepunkt im Verlauf der Bremsdrehzahl im unteren Drittel der Betriebsdrehzahl liegt.
• Kürzester Anhalteweg wird erreicht, wenn der Wendepunkt im oberen Drittel liegt. -> höhere Zeitkonstante -> höherer Widerstandswert

Anhaltezeit bei Widerstands-Bremsung.PNG

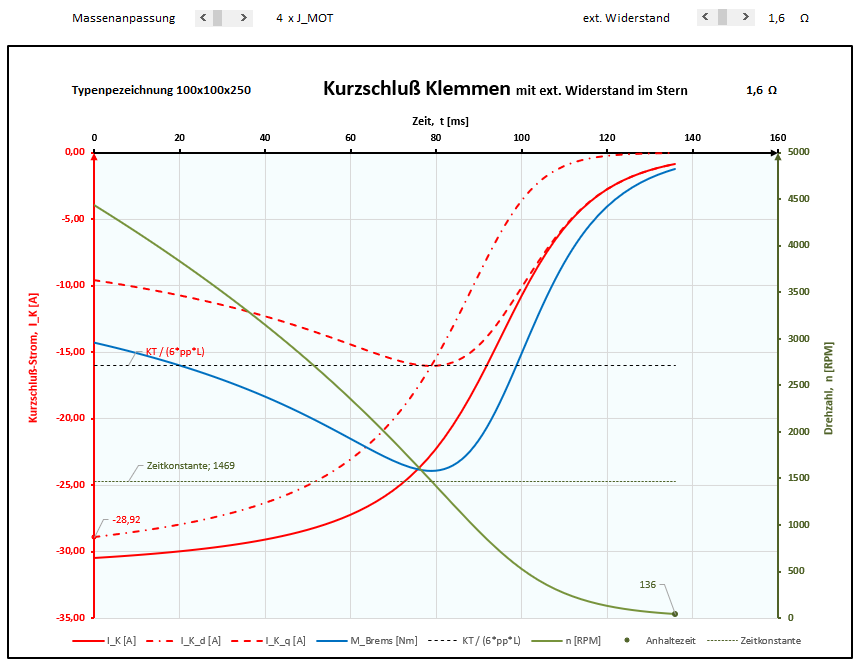
Der berechnete Verlauf berücksichtigt NICHT:

• ein zusätzliches Bremsmoment einer mechanischen Bremse
• die zusätzlichen Verluste aus VISCOUS FRICTION und STATIC-FRICTON und Wellendichtring
• die Situation bei hängenden Achsen (zusätzliche potentielle Hubenergie der Mechanik)

Die Beschaltung der induzieren Spannung ist (wie oben dargestellt) ein RL-Filter 1.Ordnung mit -20 dB/Dekade:

Übertragungsfunktion Widerstands-Bremsung.PNG

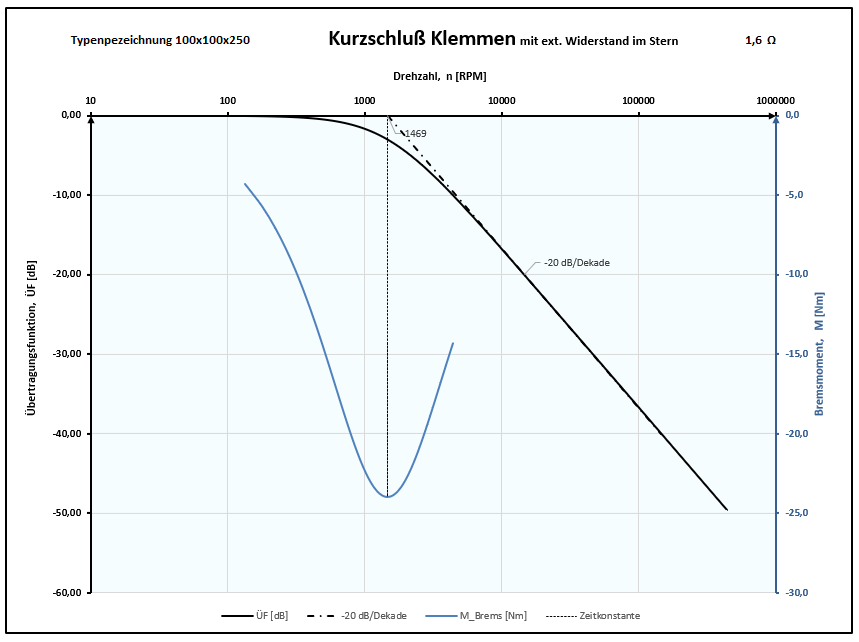
Übertragungsfunktion ÜF [db] = 20 * log ( IK / [ UEMK / (R PH + R EXT) ] )

Das Zeigerdiagramm bei Zeitkonstante -> 45°

Zeigerdiagramm bei Zeitkonstante

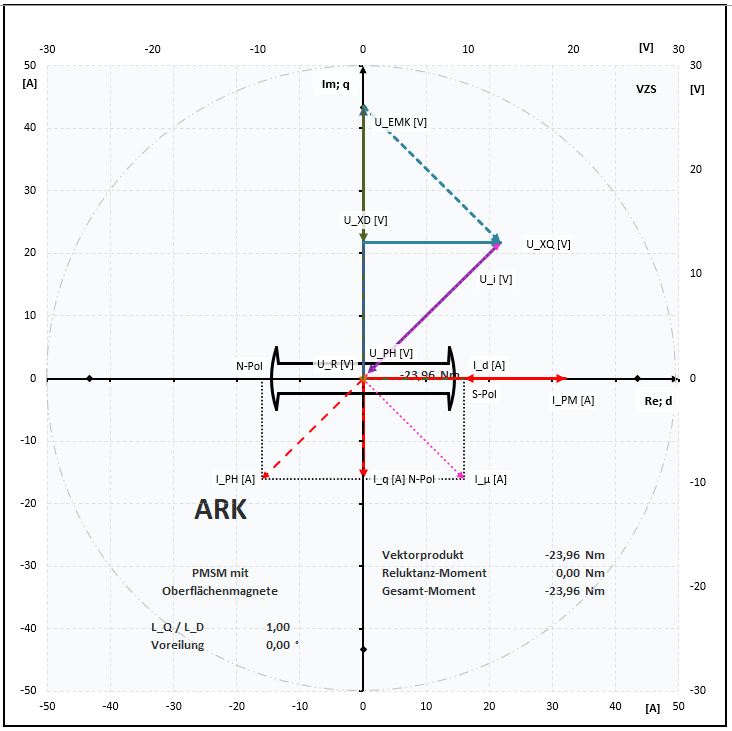
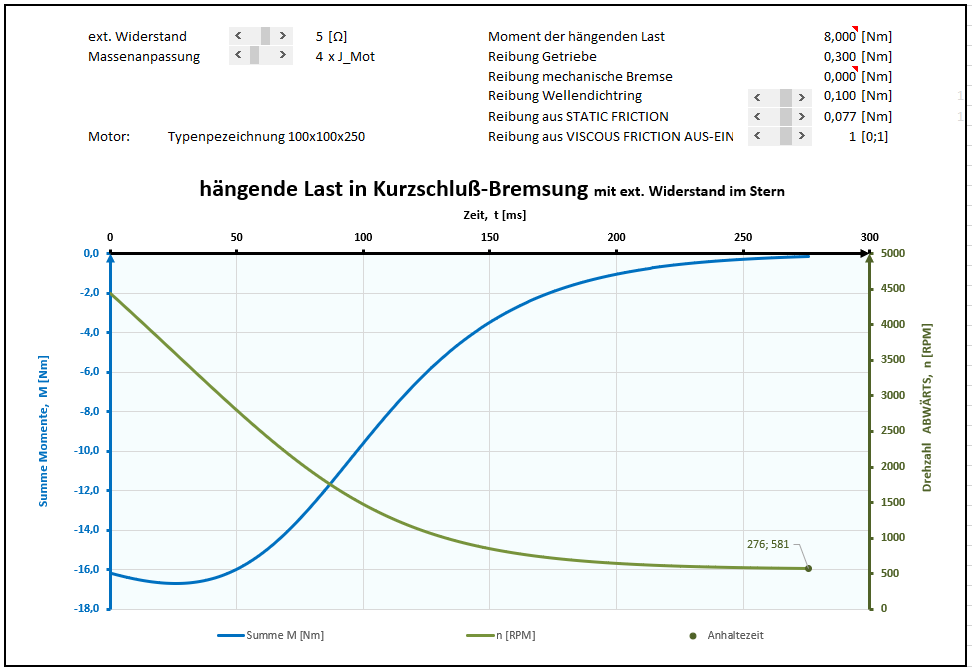
Große Trägheitsmomente oder "Hängende Last":

Die Kurzschluss- und Widerstandsbremsung findet auch Verwendung bei folgenden Applikationen:

• Abbremsen hoher Trägheitsmomente bei Netzausfall (ohne USV) um die Lebensdauer der eingebauten mechanischer Bremse zu erhöhen. Wird ein Teil der Rotationsenergie in der Kurzschluß- oder Widerstandsbremsung vernichtet, schont das die mechanische Bremse und verliert weniger Reibbelag. Zudem ist die maximale Reibarbeit pro Bremsung geringer, was die Dimensionierung der mechanischen Bremse erleichtert.
• Ist zu befürchten, daß die mechanische Bremse bei hängenden Lasten versagt, kann über die Widerstandsbremsung oder Kurzschlußbremsung eine konstante Sinkgeschwindigkeit realisiert werden, die sich nach einer gewissen Zeit einstellt. Lässt sich erreichen, daß sich eine Person in dieser Situation selbst in Sicherheit bringen kann, kann ggf auf eine redundante, zweite mechanische Bremse verzichtet werden. Hierzu ist eine gewissenhafte Sicherheitsbetrachtung notwendig.

Berechnung der Sinkgeschwindigkeit bei hängender Last

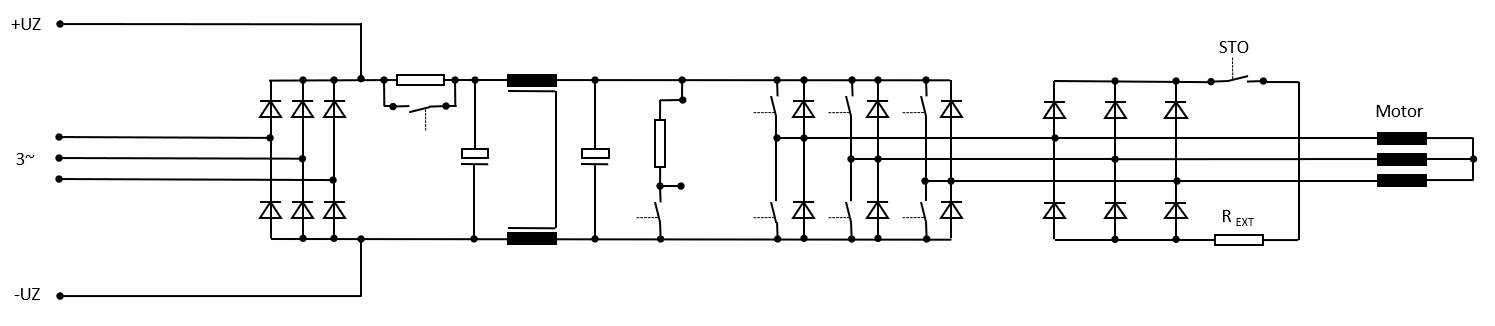
Kurzschluß über Dioden mit einem Bremswiderstand:

 Kurzschluß über Dioden

16.01.2021 R. Fetzner